),Молекулярная физика занимается изучением тепловой формы движения материи, рассматривает явления, происходящие внутри макроскопических тел. Молекулярная физика неразрывно связана с теорией строения вещества и характером движения и взаимодействия частиц составляющих вещество (молекул, атомов).
Теория, базирующаяся на положениях, что: все вещества состоят из молекул и атомов; между молекулами (атомами) существуют силы взаимодействия; молекулы и атомы находятся в непрерывном движении – называется молекулярно-кинетической. Она ставит себе целью истолковать те свойства тел, которые непосредственно наблюдаются на опыте, как суммарный результат действия большой совокупности молекул. При этом указанная теория пользуется статистическим методом, интересуясь не движением отдельных молекул, а лишь такими средними величинами, которые характеризуют движение огромной совокупности частиц. Отсюда другое ее название – статистическая физика. Молекулярная физика рассматривает движение и взаимодействие большого количества микрообъектов, составляющих макросистему; применяя законы классической механики к большому количеству микрочастиц, можно вычислить такие величины, как плотность, давление, температура, теплота, энтропия, внутренняя энергия и другие, которые являются характеристиками макросистемы.
Раздел физики, в котором изучаются соотношения между этими величинами, называется термодинамикой. Термодинамика изучает макроскопические свойства тел и явления природы, "не интересуясь" их микроскопической картиной. В основе термодинамики лежат экспериментально установленные законы, которые называют первым и вторым началами термодинамики. С помощью этих законов можно, не делая никаких предположений о молекулярном строении, изучаемых тел, получить многие сведения о свойствах тел в различных условиях.
Совокупность рассматриваемых тел, обменивающихся энергией как между собой, так и с другими (внешними) телами, называется термодинамической системой (ТДС). Состояние термодинамической системы определяется совокупностью значений всех величин, характеризующих физические свойства системы и называемых ее термодинамическими параметрами. Равновесное состояние ТДС можно задать с помощью ограниченного числа ее термодинамических параметров, которые называются параметрами системы. Между основными параметрами системы существует связь, называемая уравнением состояния.
Уравнение состояния (уравнение Менделеева-Клапейрона) идеального газа имеет вид
pV = (m/m)RT = nRT,
где m– масса газа; m --молярная масса газа; p– давление газа; V—объем газа; R—универсальная газовая постоянная; n - число молей газа; T—температура по шкале Кельвина.
Подходя к рассмотрению изменений состояния вещества с различных точек зрения, термодинамика и молекулярно-кинетическая теория взаимно дополняют друг друга, образуя, по существу, одно целое.
Как уже отмечалось, состояние системы описывается уравнением состояния. Параметры состояния системы могут изменяться, тогда говорят, что система совершает термодинамический процесс. Для термодинамических процессов установлены опытные газовые законы:
а) для изотермического процесса (T = const, m = const) – закон Бойля- Мариотта
pV = const;
б) для изобарического процесса (P = const, m = const) – закон Гей-Люссака
V/T = const,
или, используя шкалу температур Цельсия,
V = V0 (1+ ),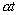
где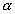 
= (1/273)(0С)-1 ;
в) для изохорического процесса (V = const, m = const) – закон Шарля
p/T = const,
или, используя шкалу температур Цельсия,
p = p0 (1+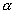
t ),
где 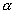= (1/273)(0С)-1 ;
г) в случае изменения трех термодинамических параметров при неизменной массе газа (m = const) – объединенный газовый закон (уравнение Клапейрона)
pV/T = const.
Закон Дальтона, определяющий давление смеси газов.
p = p1 + p2 + p3 + ... + pi +... + pn,
где pi – парциональное давление компонентов смеси; n – число компонентов смеси.
Молярная масса смеси газов
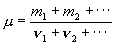
где mi – масса i-го компонента смеси; n i = mi/m i – количество вещества i-го компонента смеси; n – число компонентов смеси.
Концентрация молекул
n = N/V =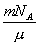 
,
где N – число молекул, содержащихся в данной системе; NA – число Авогадро; V – объем системы.
Основное уравнение кинетической теории газов
p = (2/3) n <E>,
здесь <E> - средняя кинетическая энергия поступательного движения молекул, равная (3/2) kT, где k – постоянная Больцмана.
Закон равномерного распределения энергии по степеням свободы
<E> = kT/2
и средняя полная кинетическая энергия молекулы
<E> = (i/2)kT,
где i – число степеней свободы молекулы.
Зависимость давления газа от его концентрации и температуры
p = nkT.
Распределение молекул по скоростям (распределение Максвелла)
,
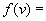
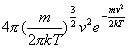где m – масса молекулы, v – ее скорость.
Средняя квадратичная скорость молекул
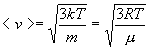
Средняя арифметическая скорость молекул
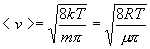
Наиболее вероятная скорость молекул
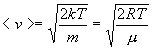
Распределение молекул по координатам (распределение Больцмана)
,
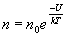где U – потенциальная энергия молекулы, n – концентрация молекул.
Барометрическая формула
.
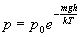Здесь p – давление.
Первое начало термодинамики
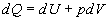
где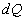 
– теплота, сообщенная газу; 
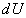– изменение внутренней энергии газа; 
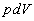– работа, совершаемая газом, против внешних сил.
Работа, совершаемая газом при его расширении,
A = P(V2 - V1) – при изобарическом процессе;
A = (m/m)RT ln(V2/V1) – при изотермическом процессе;
A = - DU = - (m/m)CV DT или A = ((RT)/(g-1))(m/m)[1- (V1/V2)g-1] – при адиабатном процессе.
КПД идеальной тепловой машины
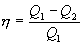, или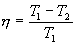 
где Q1 – теплота, полученная рабочим телом от нагревателя, Q2 – теплота, переданная рабочим телом холодильнику, T1 и T2 – температуры нагревателя и холодильника.
Связь между удельной (с) и молярной (С) теплоемоемкостями
c = C/m
Уравнение Майера
CP - CV = R ,
где CP – молярная теплоемкость при постоянном давлении и CV – молярная теплоемкость при постоянном объеме.
Удельные теплоемкости газа при постоянном объеме (cV) и постоянном давлении (cP)
cV = (i/2)(R/m), cP = ((i+2)/2)(R/m)
Уравнение Пуассона (уравнение адиабаты)(m = const, DQ = 0)
pV g = const,
где g = cР/cV – показатель адиабаты.
Внутренняя энергия идеального газа
U = (m/m)(i/2)RT = (m/m)CVT.
